High-Performance Graphics 2015 Paper

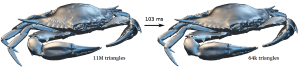Hélène Legrand, Tamy Boubekeur – Telecom ParisTech -“Morton Integrals for High Speed Geometry Simplification”. Real time geometry processing has progressively reached a performance level that makes a number of signal-inspired primitives practical for on-line applications scenarios.  This often comes through the  joint  design  of  operators,  data  structure  and  even  dedicated hardware.   Among  the  major  classes  of  geometric  operators,  filtering and super-sampling (via tessellation) have been successfully expressed  under  high-performance  constraints.   The  subsampling operator i.e., adaptive simplification, remains however a challenging  case  for  non-trivial  input  models.   In  this  paper,  we  build  a fast geometry simplification algorithm over a new concept:  Morton Integrals.  By summing up quadric error metric matrices along Morton-ordered surface samples,  we can extract concurrently the nodes of an adaptive cut in the so-defined implicit hierarchy, and optimize  all  simplified  vertices  in  parallel.
This  approach  is  inspired by integral images and exploits recent advances in high performance spatial hierarchy construction and traversal.  As a result, our  GPU  implementation  can  downsample  a  mesh  made  of  sev eral millions of polygons at interactive rates, while providing better quality than uniform simplification and preserving important salient eatures. We present results for surface meshes, polygon soups and point clouds, and discuss variations of our approach to account for per-sample attributes and alternatives error metrics.(PDF)