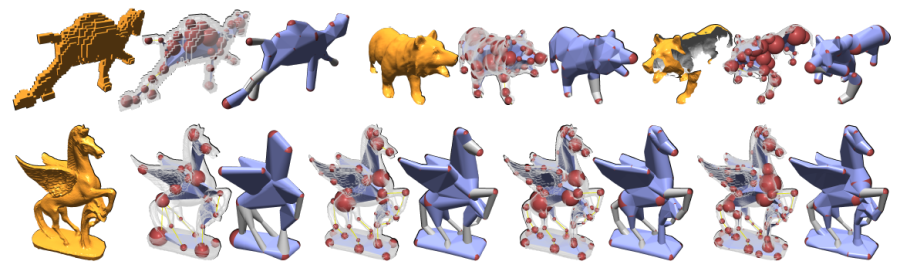
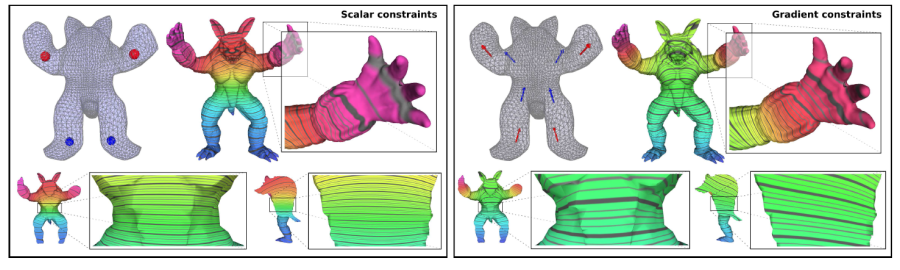
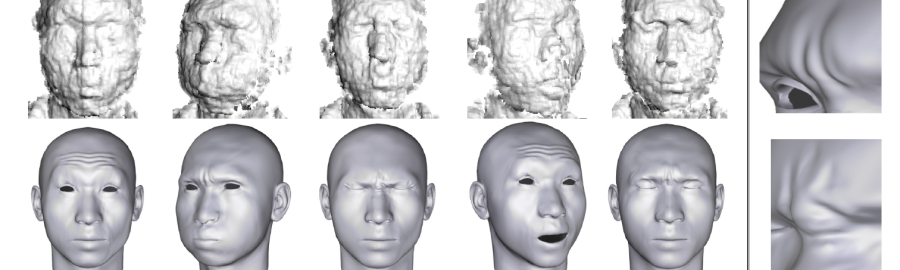
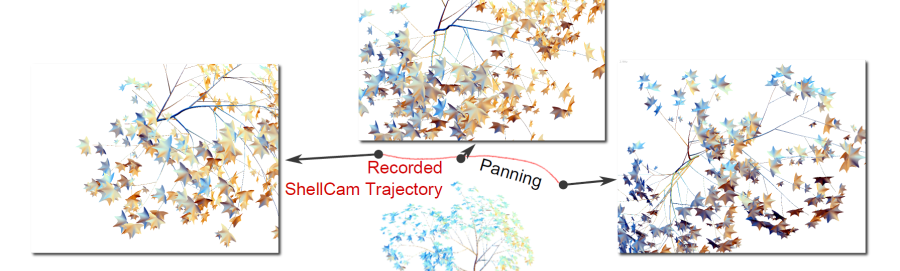
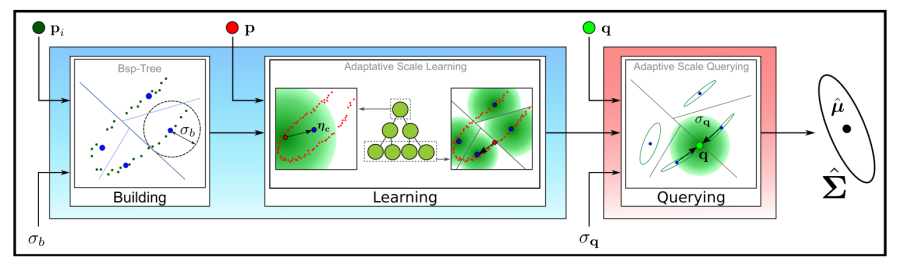
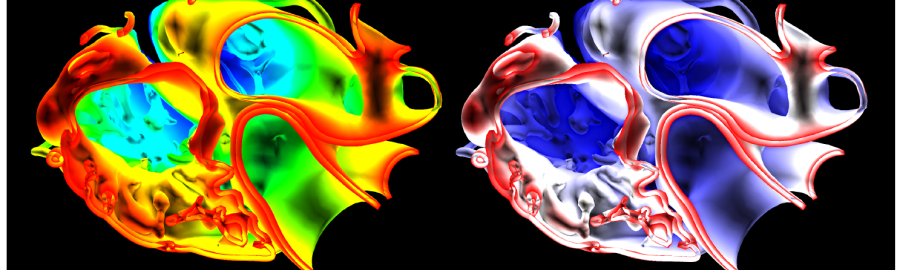
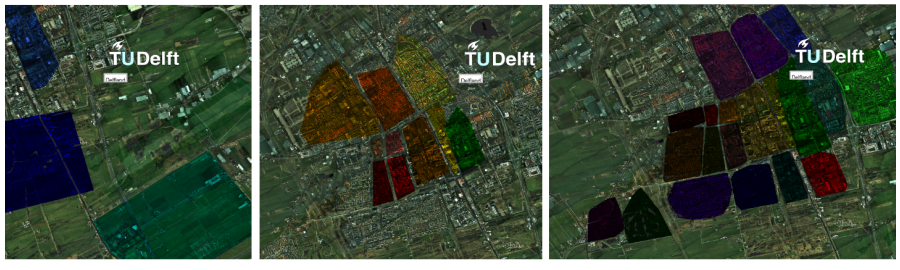
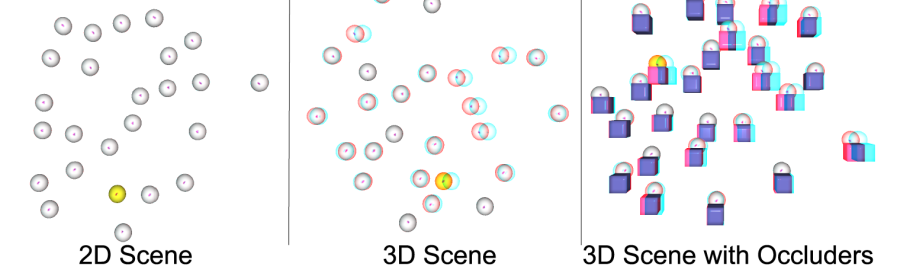
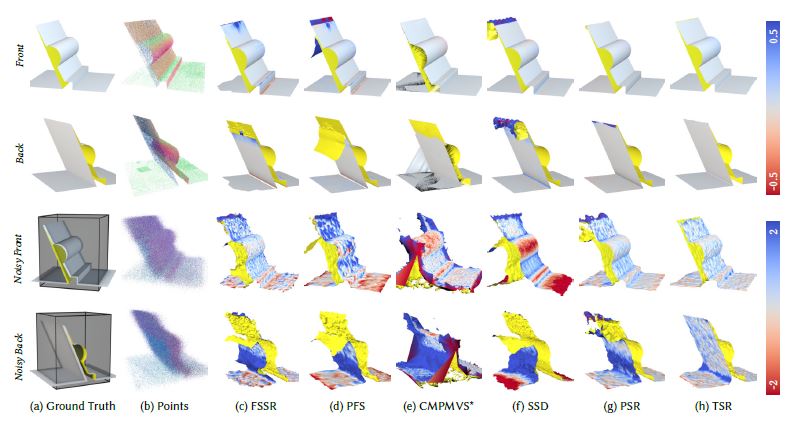
The current acquisition pipeline for visual models of 3D worlds is based on a paradigm of planning a goal-oriented acquisition – sampling on site – processing. The digital model of an artifact (an object, a building, up to an entire city) is produced by planning a specific scanning campaign, carefully selecting the (often costly) acquisition devices, performing the on-site acquisition at the required resolution and then post-processing the acquired data to produce a beautified triangulated and textured model. However, in the future we will be faced with the ubiquitous availability of sensing devices that deliver different data streams that need to be processed and displayed in a new way, for example smartphones, commodity stereo cameras, cheap aerial data acquisition devices, etc. more